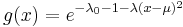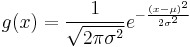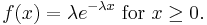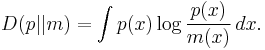Differential entropy
Differential entropy (also referred to as continuous entropy) is a concept in information theory that extends the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuous probability distributions.
Contents |
Definition
Let X be a random variable with a probability density function f whose support is a set 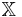 . The differential entropy
. The differential entropy 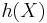 or
or 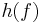 is defined as
is defined as
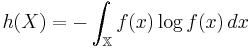 .
.
As with its discrete analog, the units of differential entropy depend on the base of the logarithm, which is usually 2 (i.e., the units are bits). See logarithmic units for logarithms taken in different bases. Related concepts such as joint, conditional differential entropy, and relative entropy are defined in a similar fashion.
One must take care in trying to apply properties of discrete entropy to differential entropy, since probability density functions can be greater than 1. For example, Uniform(0,1/2) has negative differential entropy 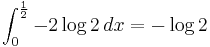 .
.
Thus, differential entropy does not share all properties of discrete entropy.
Note that the continuous mutual information 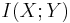 has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps) ,[1] including linear [2] transformations of X and Y, and still represents the amount of discrete information that can be transmitted over a channel that admits a continuous space of values.
has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps) ,[1] including linear [2] transformations of X and Y, and still represents the amount of discrete information that can be transmitted over a channel that admits a continuous space of values.
Properties of differential entropy
- For two densities f and g,
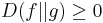 with equality if
with equality if 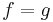 almost everywhere. Similarly, for two random variables X and Y,
almost everywhere. Similarly, for two random variables X and Y, 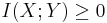 and
and 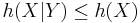 with equality if and only if X and Y are independent.
with equality if and only if X and Y are independent. - The chain rule for differential entropy holds as in the discrete case
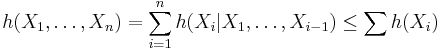 .
.
- Differential entropy is translation invariant, ie,
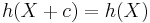 for a constant c.
for a constant c. - Differential entropy is in general not invariant under arbitrary invertible maps. In particular, for a constant a,
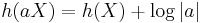 . For a vector valued random variable X and a matrix A,
. For a vector valued random variable X and a matrix A, 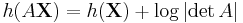 .
. - In general, for a transformation from a random vector X to a random vector with same dimension Y
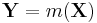 , the corresponding entropies are related via
, the corresponding entropies are related via 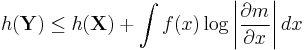 where
where 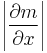 is the Jacobian of the transformation m. Equality is achieved if the transform is bijective, i.e., invertible.
is the Jacobian of the transformation m. Equality is achieved if the transform is bijective, i.e., invertible. - If a random vector
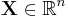 has mean zero and covariance matrix K,
has mean zero and covariance matrix K, ![h(\mathbf{X}) \leq \frac{1}{2} \log[(2\pi e)^n \det{K}]](/2012-wikipedia_en_all_nopic_01_2012/I/503ffc96241b2575bfd151ab39010225.png) with equality if and only if X is jointly gaussian.
with equality if and only if X is jointly gaussian.
However, differential entropy does not have other desirable properties:
- It is not invariant under change of variables.
- It can be negative.
A modification of differential entropy that addresses this is the relative information entropy, also known as the Kullback–Leibler divergence, which includes an invariant measure factor (see limiting density of discrete points).
Maximization in the normal distribution
With a normal distribution, differential entropy is maximized for a given variance. The following is a proof that a Gaussian variable has the largest entropy amongst all random variables of equal variance.
Let 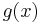 be a Gaussian PDF with mean
be a Gaussian PDF with mean  and variance
and variance 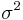 and
and  an arbitrary PDF with the same variance. Since differential entropy is translation invariant we can assume that
an arbitrary PDF with the same variance. Since differential entropy is translation invariant we can assume that  has the same mean of
has the same mean of  as
as 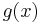 .
.
Consider the Kullback-Leibler divergence between the two distributions
Now note that
because the result does not depend on  other than through the variance. Combining the two results yields
other than through the variance. Combining the two results yields
with equality when  following from the properties of Kullback-Leibler divergence.
following from the properties of Kullback-Leibler divergence.
This result may also be demonstrated using the variational calculus. A Lagrangian function with two Lagrangian multipliers may be defined as:
where g(x) is some function with mean μ. When the entropy of g(x) is at a maximum and the constraint equations, which consist of the normalization condition 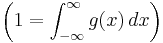 and the requirement of fixed variance
and the requirement of fixed variance 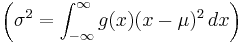 , are both satisfied, then a small variation
, are both satisfied, then a small variation 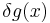 about g(x) will produce a variation
about g(x) will produce a variation 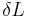 about L which is equal to zero:
about L which is equal to zero:
Since this must hold for any small 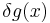 , the term in brackets must be zero, and solving for g(x) yields:
, the term in brackets must be zero, and solving for g(x) yields:
Using the constraint equations to solve for 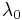 and
and  yields the normal distribution:
yields the normal distribution:
Example: Exponential distribution
Let X be an exponentially distributed random variable with parameter  , that is, with probability density function
, that is, with probability density function
Its differential entropy is then
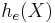 |
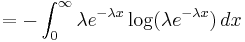 |
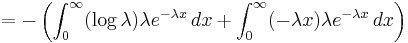 |
|
![= -\log \lambda \int_0^\infty f(x)\,dx %2B \lambda E[X]](/2012-wikipedia_en_all_nopic_01_2012/I/111f140bd026b08482d9840334508dfd.png) |
|
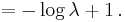 |
Here, 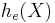 was used rather than
was used rather than 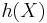 to make it explicit that the logarithm was taken to base e, to simplify the calculation.
to make it explicit that the logarithm was taken to base e, to simplify the calculation.
Differential entropies for various distributions
In the table below, 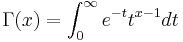 (the gamma function),
(the gamma function), 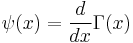 ,
, 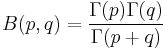 , and
, and 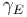 is Euler's constant. Each distribution maximizes the entropy for a particular set of functional constraints listed in the fourth column, and the constraint that x be included in the support of the probability density, which is listed in the fifth column.[3]
is Euler's constant. Each distribution maximizes the entropy for a particular set of functional constraints listed in the fourth column, and the constraint that x be included in the support of the probability density, which is listed in the fifth column.[3]
| Distribution Name | Probability density function (pdf) | Entropy in nats | Maximum Entropy Constraint | Support |
|---|---|---|---|---|
| Uniform | 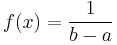 |
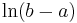 |
None | ![[a,b]\,](/2012-wikipedia_en_all_nopic_01_2012/I/7f3408c72246eece3d5542fc853ce417.png) |
| Normal | 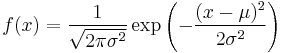 |
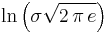 |
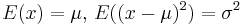 |
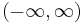 |
| Exponential | 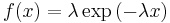 |
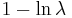 |
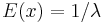 |
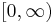 |
| Rayleigh | 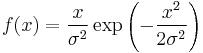 |
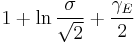 |
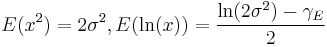 |
 |
| Beta | 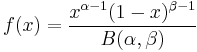 for for 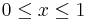 |
![\ln B(\alpha,\beta) - (\alpha-1)[\psi(\alpha) - \psi(\alpha %2B\beta)]\,](/2012-wikipedia_en_all_nopic_01_2012/I/34dad70ac931f39ca86988327d521608.png) ![- (\beta-1)[\psi(\beta) - \psi(\alpha %2B \beta)] \,](/2012-wikipedia_en_all_nopic_01_2012/I/618397c7e55ce77406a00a6d8d7002a7.png) |
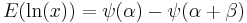 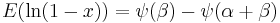 |
![[0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/d09694b77d8a3a03f6879fa37f09d0b0.png) |
| Cauchy | 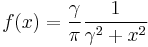 |
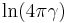 |
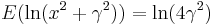 |
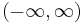 |
| Chi | 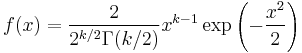 |
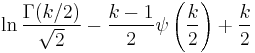 |
![E(x^2)=k,\,E(\ln(x))=\frac{1}{2}\left[\psi\left(\frac{k}{2}\right)\!%2B\!\ln(2)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/c62fb3602aaa16e4e64d95214083c1e3.png) |
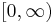 |
| Chi-squared | 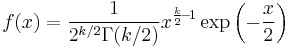 |
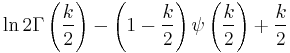 |
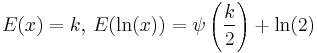 |
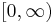 |
| Erlang | 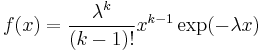 |
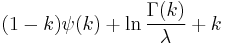 |
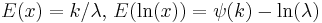 |
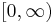 |
| F | 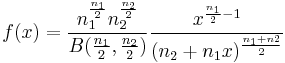 |
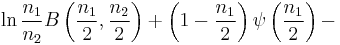 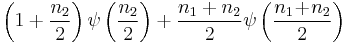 |
 |
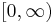 |
| Gamma | 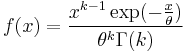 |
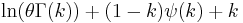 |
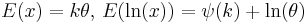 |
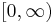 |
| Laplace | 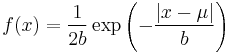 |
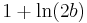 |
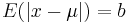 |
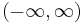 |
| Logistic | 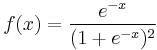 |
 |
 |
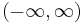 |
| Lognormal | 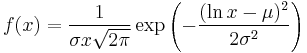 |
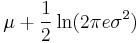 |
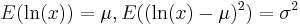 |
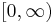 |
| Maxwell-Boltzmann | 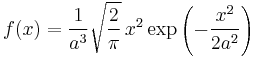 |
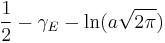 |
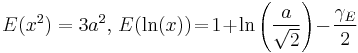 |
 |
| Generalized normal | 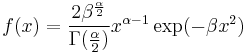 |
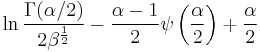 |
 |
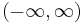 |
| Pareto | 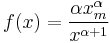 |
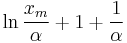 |
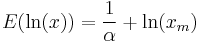 |
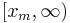 |
| Student's t | 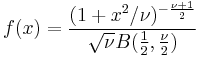 |
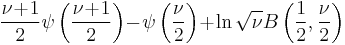 |
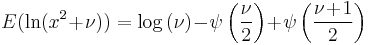 |
 |
| Triangular | 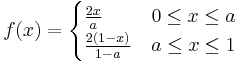 |
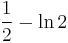 |
 |
![[0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/d09694b77d8a3a03f6879fa37f09d0b0.png) |
| Weibull | 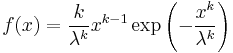 |
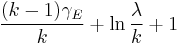 |
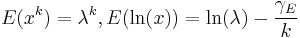 |
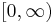 |
| Multivariate normal | 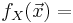 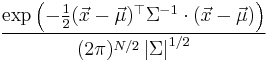 |
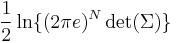 |
 |
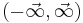 |
(Many of the differential entropies are from.[4]
Variants
As described above, differential entropy does not share all properties of discrete entropy. A modification of differential entropy adds an invariant measure factor to correct this, (see limiting density of discrete points). If m(x) is further constrained to be a probability density, the resulting notion is called relative entropy in information theory:
The definition of differential entropy above can be obtained by partitioning the range of X into bins of length  with associated sample points ih within the bins, for X Riemann integrable. This gives a quantized version of X, defined by
with associated sample points ih within the bins, for X Riemann integrable. This gives a quantized version of X, defined by 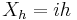 if
if 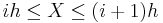 . Then the entropy of
. Then the entropy of 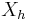 is
is
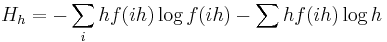 .
.
The first term on the right approximates the differential entropy, while the second term is approximately 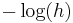 . Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be
. Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be 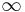 .
.
See also
- Information entropy
- Information theory
- Limiting density of discrete points
- Self-information
- Kullback-Leibler divergence
- Entropy estimation
References
- ^ Kraskov, Alexander; Stögbauer, Grassberger (2004). "Estimating mutual information". Phys. Rev. E 60: 066138. arXiv:cond-mat/0305641. Bibcode 2004PhRvE..69f6138K. doi:10.1103/PhysRevE.69.066138.
- ^ Fazlollah M. Reza (1961, 1994). An Introduction to Information Theory. Dover Publications, Inc., New York. ISBN 0-486-68210-2. http://books.google.com/books?id=RtzpRAiX6OgC&pg=PA8&dq=intitle:%22An+Introduction+to+Information+Theory%22++%22entropy+of+a+simple+source%22&as_brr=0&ei=zP79Ro7UBovqoQK4g_nCCw&sig=j3lPgyYrC3-bvn1Td42TZgTzj0Q.
- ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model". Journal of Econometrics (Elsevier): 219–230. http://www.wise.xmu.edu.cn/Master/Download/..%5C..%5CUploadFiles%5Cpaper-masterdownload%5C2009519932327055475115776.pdf. Retrieved 2011-06-02.
- ^ Lazo, A. and P. Rathie. On the entropy of continuous probability distributions Information Theory, IEEE Transactions on, 1978. 24(1): p. 120-122.
- Thomas M. Cover, Joy A. Thomas. Elements of Information Theory New York: Wiley, 1991. ISBN 0-471-06259-6
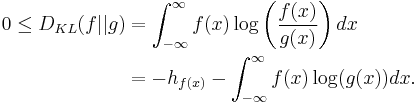
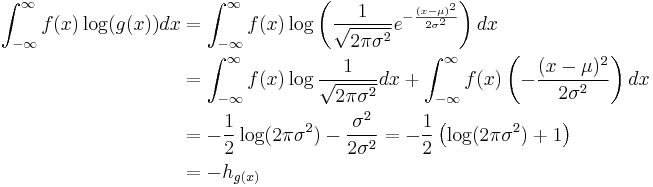
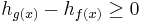
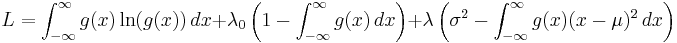
![0=\delta L=\int_{-\infty}^\infty \delta g(x)\left[\ln(g(x))%2B1%2B\lambda_0%2B\lambda(x-\mu)^2\right]\,dx](/2012-wikipedia_en_all_nopic_01_2012/I/8243c56feefb7e56b0c273a0d251ae97.png)